Machine learning for package users with R (5): Random Forest

Random Forest is still one of the strongest supervised learning methods although these days many people love to use Deep Learning or Convolutional NN. Of course because it's simple architecture and a lot of implementation in various environments or languages, e.g. Python, R.

The point I wanna emphasize here is that Random Forest is also a strong method for not only classification but also estimation of variable importance, derived from its origin, decision / regression tree.

A brief trial on a short version of MNIST datasets

Below is a result on the short hold-out version of MNIST data. In this example I only tuned the number of variables of Random Forest using tuneRF() function, but the result was great.

> train<-read.csv("short_prac_train.csv")
> test<-read.csv("short_prac_test.csv")
> train$label<-as.factor(train$label)
> test$label<-as.factor(test$label)
> library(randomForest)

# Tune Random Forest
> tuneRF(train[,-1],train[,1],doBest=T)
mtry = 28  OOB error = 8.64% 
Searching left ...
mtry = 14 	OOB error = 9.28% 
-0.07407407 0.05 
Searching right ...
mtry = 56 	OOB error = 8.5% 
0.0162037 0.05 

# took too much and manually terminated
# "mtry", the number of randomly chosen independent variables, should be 56

> train.rf<-randomForest(label~.,train,mtry=56)
> table(test$label,predict(train.rf,newdata=test[,-1]))
   
     0  1  2  3  4  5  6  7  8  9
  0 96  0  0  0  0  0  3  0  1  0
  1  0 98  0  0  0  0  0  1  1  0
  2  0  0 96  1  1  0  1  1  0  0
  3  0  0  0 90  0  3  1  1  3  2
  4  0  1  0  0 94  0  1  0  0  4
  5  1  0  0  1  0 97  1  0  0  0
  6  0  0  1  0  0  2 96  0  1  0
  7  0  0  0  0  1  0  0 95  0  4
  8  0  1  1  2  0  1  0  0 95  0
  9  0  0  0  0  2  1  0  1  0 96
> sum(diag(table(test$label,predict(train.rf,newdata=test[,-1]))))/nrow(test)
[1] 0.953

This took much shorter time but its performance great and better than SVM or NN. Accuracy 0.953 on this hold-out MNIST dataset is almost the same as Deep Learning implemented in H2O. You can easily understand why many people love to use Random Forest.

Algorithm summary

As repeatedly mentioned in this blog, we have a great online textbook: ESL. See p.588 for an algorithm of Random Forest.

1. For $b = 1$ to $B$ :

(a) Draw a bootstrap sample $\mathbf{Z^*}$ of size $N$ from the training data.

(b) Grow a random-forest tree $T_b$ to the bootstrapped data, by recursively repeating the following steps for each terminal node of the tree, until the minimum node size $n_{min}$ is reached.

i. Select $m$ variables at random from the $p$ variables.
ii. Pick the best variable/split-point among the $m$ .
iii. Split the node into two daughter nodes.

2. Output the ensemble of trees $\{T_b\}^B_1$ .

To make a prediction at a new point $x$ :

Regression: $\hat{f}^B_{rf}(x) = \frac{1}{B}\sum^B_{n=1}T_b(x)$

Classification: Let $\hat{C}_b(x)$ be the class prediction of the $b$ th random-forest tree. Then $\hat{C}^B_{rf}(x) = majority ~ vote \{ \hat{C}_b(x)\}^B_1$ .

In short, Random Forest is one of bagging methods. Unlike the other bagging methods, its weak classifier is a "de-correlated" decision / regression tree, in order to decrease correlation between subspaces and to avoid overfitting.

f:id:TJO:20150603222152p:plain

I think a schematic figure above well explains how Random Forest works. At any rate, the algorithm generates a lot of weak decision / regression trees and finally their outputs are converged with a certain prefixed rule. Its consequent output would be less overfitted and well generalized, as assumed.

How it works on XOR patterns and linearly separable patterns

OK, let's see what kind of decision boundaries Random Forest draws. In case of XOR patterns, run as below.

# Import the library
> library(randomForest)

# Set up datasets
> xors<-read.table("xor_simple.txt",header=T)
> xors$label<-as.factor(xors$label-1)
> xorc<-read.table("xor_complex.txt",header=T)
> xorc$label<-as.factor(xorc$label-1)

# Run randomForest() function
> xors.rf<-randomForest(label~.,xors)
> xorc.rf<-randomForest(label~.,xorc)

# Set up a grid
> px<-seq(-4,4,0.03)
> py<-seq(-4,4,0.03)
> pgrid<-expand.grid(px,py)
> names(pgrid)<-names(xors)[-3]

# Draw on simple XOR pattern
> plot(c(),type='n',xlim=c(-4,4),ylim=c(-4,4))
> par(new=T)
> rect(0,0,4,4,col='#ddddff')
> par(new=T)
> rect(-4,0,0,4,col='#ffdddd')
> par(new=T)
> rect(-4,-4,0,0,col='#ddddff')
> par(new=T)
> rect(0,-4,4,0,col='#ffdddd')
> par(new=T)
> plot(xors[,-3],col=c(rep('blue',50),rep('red',50)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2.5)
> par(new=T)
> contour(px,py,array(predict(xors.rf,newdata=pgrid),dim = c(length(px),length(py))),levels = 0.5,drawlabels = T,col='purple',lwd=6,xlim=c(-4,4),ylim=c(-4,4))

# Draw on complex XOR pattern
> plot(c(),type='n',xlim=c(-4,4),ylim=c(-4,4))
> par(new=T)
> rect(0,0,4,4,col='#ddddff')
> par(new=T)
> rect(-4,0,0,4,col='#ffdddd')
> par(new=T)
> rect(-4,-4,0,0,col='#ddddff')
> par(new=T)
> rect(0,-4,4,0,col='#ffdddd')
> par(new=T)
> plot(xorc[,-3],col=c(rep('blue',50),rep('red',50)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2.5)
> par(new=T)
> contour(px,py,array(predict(xorc.rf,newdata=pgrid),dim = c(length(px),length(py))),levels = 0.5,drawlabels = T,col='purple',lwd=6,xlim=c(-4,4),ylim=c(-4,4))

f:id:TJO:20150604123646p:plain:w250 f:id:TJO:20150604123656p:plain:w250

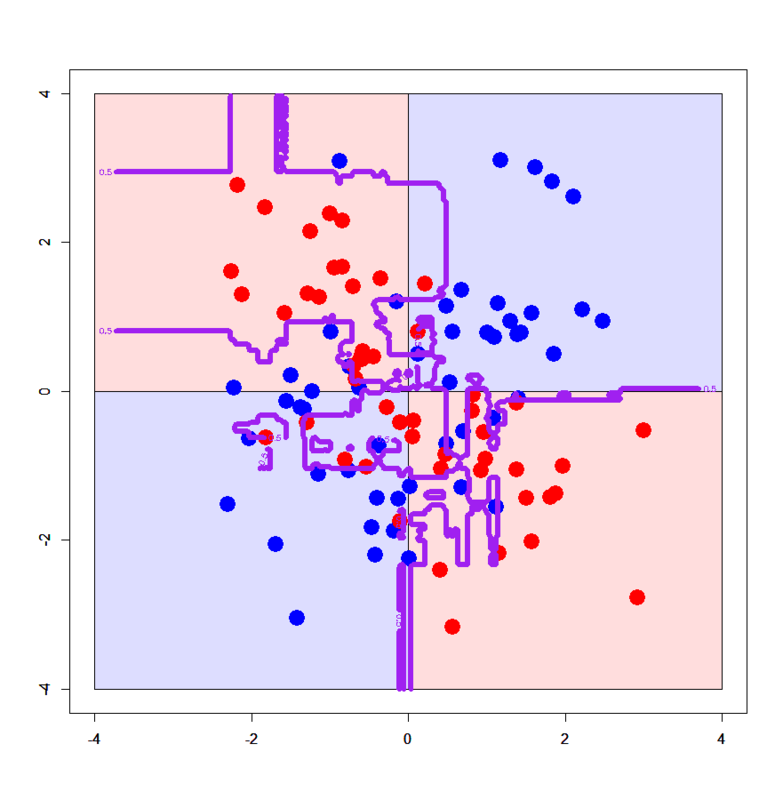
The former one looks like the one by Decision Tree (Machine learning for package users with R (1): Decision Tree - Data Scientist in Ginza, Tokyo), but the latter one looks too much overfitted... What? The algorithm above emphasizes it can strongly avoid overfitting???

Yes, just empirically (from my own experience) it has been known that Random Forest sometimes overfits more than expected. In the case of 2D XOR patterns the number of variables ("mtry" here) is just 2 so tuning on independent variables almost never works, but in many cases it would work very efficiently.

In R, you can easily tune it with tuneRF() function in order to decide an optimal value of "mtry" and you can use it in randomForest() function with "mtry" argument. In the example with a hold-out MNIST dataset above, "mtry" was 56 out of 784.

On the other hand, let's see how RF works on linearly separable datasets.

# Set up linearly separable datasets
> dbi<-read.table("linear_bi.txt",header=T)
> dbi$label<-as.factor(dbi$label)
> dml<-read.table("linear_multi.txt",header=T)
> dml$label<-as.factor(dml$label)

# Set up a grid
> px2<-seq(-0.5,4.5,0.02)
> py2<-seq(-0.5,4.5,0.02)
> pgrid2<-expand.grid(px2,py2)
> names(pgrid2)<-names(dbi)[-3]

# Fit models
> dbi.rf<-randomForest(label~.,dbi)
> dml.rf<-randomForest(label~.,dml)

# Draw on 2-classes linearly separable pattern
> plot(c(),type='n',xlim=c(-0.5,3.5),ylim=c(-0.5,3.5))
> par(new=T)
> polygon(c(-0.5,-0.5,3.5),c(3.5,-0.5,-0.5),col='#ddddff')
> par(new=T)
> polygon(c(-0.5,3.5,3.5),c(3.5,-0.5,3.5),col='#ffdddd')
> par(new=T)
> plot(dbi[,-3],pch=19,col=c(rep('blue',25),rep('red',25)),cex=3,xlim=c(-0.5,3.5),ylim=c(-0.5,3.5))
> par(new=T)
> contour(px2,py2,array(predict(dbi.rf,newdata=pgrid2),dim = c(length(px2),length(py2))),xlim=c(-0.5,3.5),ylim=c(-0.5,3.5),lwd=6,col='purple',levels = 0.5,drawlabels = T)

# Draw on 3-classes linearly separable pattern
> plot(c(),type='n',xlim=c(-0.5,4.5),ylim=c(-0.5,4.5))
> par(new=T)
> polygon(c(-0.5,-0.5,3.5),c(3.5,-0.5,-0.5),col='#ddddff')
> par(new=T)
> polygon(c(-0.5,3.5,4.5,4.5,1.0,-0.5),c(3.5,-0.5,-0.5,1.0,4.5,4.5),col='#ffdddd')
> par(new=T)
> polygon(c(1.0,4.5,4.5),c(4.5,1.0,4.5),col='#ddffdd')
> par(new=T)
> plot(dml[,-3],pch=19,col=c(rep('blue',25),rep('red',25),rep('green',25)),cex=3,xlim=c(-0.5,4.5),ylim=c(-0.5,4.5))
> par(new=T)
> contour(px2,py2,array(predict(dml.rf,newdata=pgrid2,type='class'),dim=c(length(px2),length(py2))),xlim=c(-0.5,4.5),ylim=c(-0.5,4.5),col="purple",lwd=6,drawlabels=T)

f:id:TJO:20150604145442p:plain:w250 f:id:TJO:20150604145454p:plain:w250

LOL neither decision boundaries go along with the assumed true boundaries. I think this characteristic of Random Forest may be derived from that of Decision Tree. It means that even Random Forest has difficulty in classification on linearly separable patterns.

Conclusions

Important lessons learned here are as follows:

Random Forest performs very well in general, comparable with even Deep Learning
Tuning on "mtry" parameter is important
RF seems to easily get overfitted
Similar to Decision Tree, RF is bad at classifying linearly separable patterns

Although there are some disadvantages in RF, many people really love to apply it to real-world data... for example user classification in CRM systems or customer targeting in demand-side platform (DSP) of Internet ads. Its algorithm is much simple and easy to implement, so many engineers implement it not only with packages or libraries but also from scratch.

...OK, in the next post will be the final one on supervised classifier - I'll write about Xgboost (eXtreme Gradient Boosting) that is currently the most popular classifier in Kaggle or other ML competitions.