Machine learning for package users with R (6): Xgboost (eXtreme Gradient Boosting)

As far as I've known, Xgboost is the most successful machine learning classifier in several competitions in machine learning, e.g. Kaggle or KDD cups. Indeed the team winning Higgs-Boson competition used Xgboost and below is their code release.

<a href="https://www.kaggle.com/c/higgs-boson/forums/t/10425/code-release">Code release - Higgs Boson Machine Learning Challenge | Kaggle</a>

Very fortunately, we have a good implementation for R or Python and it's distributed via GitHub. You can get it from the link below.

<a href="https://github.com/dmlc/xgboost">dmlc/xgboost</a>

{xgboost} package is now out of CRAN so you have to install it with {devtools} package. README.md of the GitHub repository above shows how to install and you can easily do it.

A brief trial on a short version of MNIST datasets

Of course you may expect Xgboost will work well on our short hold-out version of MNIST datasets. Let's see its performance.

> library(xgboost)
> library(Matrix)
> train<-read.csv("short_prac_train.csv")
> test<-read.csv("short_prac_test.csv")
> train.mx<-sparse.model.matrix(label~., train)
> test.mx<-sparse.model.matrix(label~., test)
> dtrain<-xgb.DMatrix(train.mx, label=train$label)
> dtest<-xgb.DMatrix(test.mx, label=test$label)
> train.gdbt<-xgb.train(params=list(objective="multi:softmax", num_class=10, eval_metric="mlogloss", eta=0.2, max_depth=5, subsample=1, colsample_bytree=0.5), data=dtrain, nrounds=150, watchlist=list(eval=dtest, train=dtrain))
[0]	eval-mlogloss:1.738412	train-mlogloss:1.698857
[1]	eval-mlogloss:1.445343	train-mlogloss:1.381565
[2]	eval-mlogloss:1.238927	train-mlogloss:1.152097

# ...

[148]	eval-mlogloss:0.154864	train-mlogloss:0.002696
[149]	eval-mlogloss:0.155017	train-mlogloss:0.002677
> pred<-predict(train.gdbt,newdata=dtest)
> sum(diag(table(test$label,pred)))/nrow(test)
[1] 0.958

Accuracy 0.958 is superior to Random Forest and exactly the same as Deep Learning with H2O. This is why many ML competitors love Xgboost as well as Deep Learning I think.

Algorithm summary

In principle, Xgboost is a variation of boosting. In Wikipedia, boosting is defined as below.

While boosting is not algorithmically constrained, most boosting algorithms consist of iteratively learning weak classifiers with respect to a distribution and adding them to a final strong classifier. When they are added, they are typically weighted in some way that is usually related to the weak learners' accuracy. After a weak learner is added, the data is reweighted: examples that are misclassified gain weight and examples that are classified correctly lose weight (some boosting algorithms actually decrease the weight of repeatedly misclassified examples, e.g., boost by majority and BrownBoost). Thus, future weak learners focus more on the examples that previous weak learners misclassified.
(wikipedia:en:Boosting_(machine_learning))

Different from bagging including Random Forest featured in the previous post, boosting is trained with further focusing on misclassified data points. You can see what it means in its algorithm, shown in Chapter 10 of ESL textbook.

1. Initialize $f_0 (x) = argmin_{\gamma} \sum^N_{i=1} L (y_i, \gamma)$ .

2. For $m = 1$ to $M$ :

(a) For $i = 1, 2, \cdots, N$ , compute
$r_{im} = - \left[ \frac{\partial L(y_i, f(x_i))}{\partial f(x_i)} \right]_{f=f_{m-1}}$ .

(b) Fit a regression tree to the targets $r_{im}$ giving terminal regions $R_{jm} (j = 1, 2, \cdots, J_m)$ .

(c) For $j = 1, 2, \cdots, J_m$ compute
$\gamma_{jm} = argmin_{\gamma} \displaystyle \sum_{x_i \in R_{jm}} L (y_i, f_{m-1}(x_i) + \gamma$ .

(d) Update $f_m(x) = f_{m-1}(x) + \sum^{J_m}_{j=1} \gamma_{jm} I(x \in R_{jm})$ .

3. Output $\hat{f}(x) = f_M(x)$ .

(Note: Here Regression Tree is supposed to be used, $f(x)$ is predictive function, $L(y, f(x))$ is a loss function for observation $y$ , $I(x \in R_{jm})$ is an index function giving 1 if $x$ is included in $R_{jm}$ )

If an updating part of 2.(d) is replaced with a product of (a) and some learning rate (e.g. $f_m(x) = f_{m-1}(x) - \mu r_m$ ), it becomes just a (steepest) gradient descent. But in this case of Gradient Boosting Tree algorithm, more sophisticated updating method is used; extracting only samples from misclassified region detected by (b) step and updating $f(x)$ . It's further greedier than gradient descent and usual boosting in which only weight of each sample is adjusted for subsequent weak learners.

ESL textbook describes more tips about tuning of Xgboost at p.413 or after. For example, tree size $J$ should be approximately $4 \leq J \leq 8$ and 6 would work*1, iteration $M$ should not be so large as well as early stopping of NN, 2.(d) should be changed as $f_m(x) = f_{m-1}(x) + \eta \sum^{J_m}_{j=1} \gamma_{jm} I(x \in R_{jm})$ and contribution of each tree $\nu$ should be kept within $0 \leq \nu \leq 1$ as small as 0.2 or 0.6*2, and subsampling rate $\eta$ should be kept around 0.5*3.

For further tips about parameter tuning, see comments in their GitHub:

Control Overfitting

When you observe high training accuracy, but low tests accuracy, it is likely that you encounter overfitting problem.

There are in general two ways that you can control overfitting in xgboost

The first way is to directly control model complexity

This include max_depth, min_child_weight and gamma

The second way is to add randomness to make training robust to noise

This include subsample, colsample_bytree

You can also reduce stepsize eta, but needs to remember to increase num_round when you do so.

Almost the same as the other classifiers, parameter tuning is vital. Needless to say, bad parameter tuning results in a bad result.

How it works on XOR patterns and linearly separable patterns

OK, let's see how Xgboost works on our sample datasets; first run as below for experiments on XOR patterns.

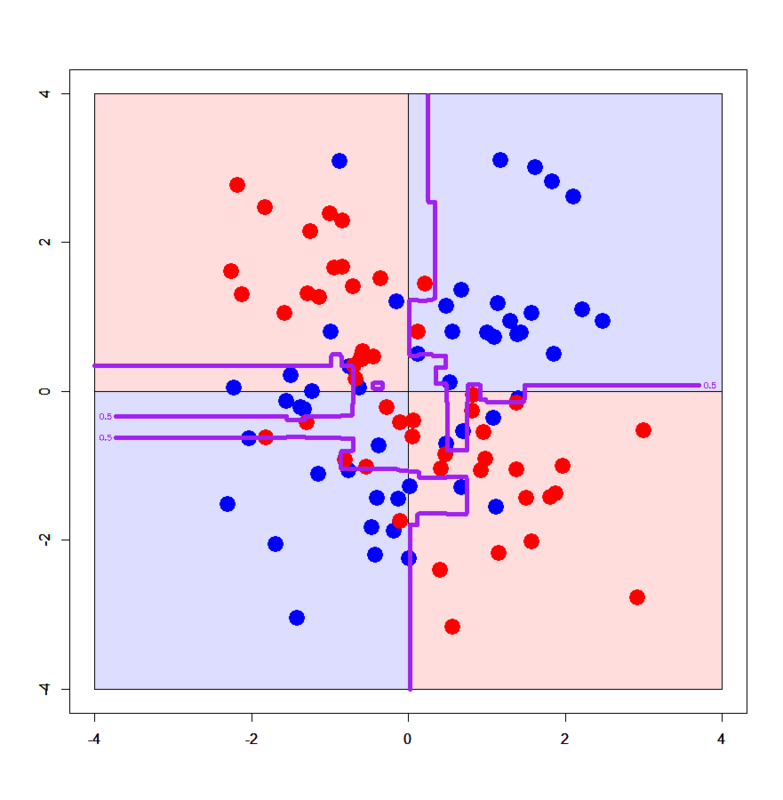
# Set up datasets of XOR patterns
> xors<-read.table("xor_simple.txt",header=T)
> xorc<-read.table("xor_complex.txt",header=T)
> xors$label<-xors$label-1
> xorc$label<-xorc$label-1

# Set up a grid
> px<-seq(-4,4,0.03)
> py<-seq(-4,4,0.03)
> pgrid1<-expand.grid(px,py)
> names(pgrid1)<-names(xors)[-3]

# Import required R packages
> library(xgboost)
> library(Matrix)

# Convert datasets into sparse.model.matrix
> xors.mx<-sparse.model.matrix(label~.,xors)
> xorc.mx<-sparse.model.matrix(label~.,xorc)
> pgrid1.mx<-sparse.model.matrix(~.,pgrid1)

# Convert them further into xgb.DMatrix
> dxors<-xgb.DMatrix(xors.mx,label=xors$label)
> dxorc<-xgb.DMatrix(xorc.mx,label=xorc$label)
> dpgrid1<-xgb.DMatrix(pgrid1.mx)

# Train xgboost models with xgb.train() function
> xors.gdbt<-xgb.train(params=list(objective="binary:logistic",eval_metric="logloss"),data=dxors,nrounds=100)
> xorc.gdbt<-xgb.train(params=list(objective="binary:logistic",eval_metric="logloss"),data=dxorc,nrounds=100)

# Draw on simple XOR pattern
> plot(c(),type='n',xlim=c(-4,4),ylim=c(-4,4))
> par(new=T)
> rect(0,0,4,4,col='#ddddff')
> par(new=T)
> rect(-4,0,0,4,col='#ffdddd')
> par(new=T)
> rect(-4,-4,0,0,col='#ddddff')
> par(new=T)
> rect(0,-4,4,0,col='#ffdddd')
> par(new=T)
> plot(xors[,-3],col=c(rep('blue',50),rep('red',50)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2.5)
> par(new=T)
> contour(px,py,array(predict(xors.gdbt,newdata=dpgrid1),dim = c(length(px),length(py))),levels = 0.5,drawlabels = T,col='purple',lwd=6,xlim=c(-4,4),ylim=c(-4,4))

# Draw on complex XOR pattern
> xorc.gdbt<-xgb.train(params=list(objective="binary:logistic",eval_metric="logloss"),data=dxorc,nrounds=100)
> plot(c(),type='n',xlim=c(-4,4),ylim=c(-4,4))
> par(new=T)
> rect(0,0,4,4,col='#ddddff')
> par(new=T)
> rect(-4,0,0,4,col='#ffdddd')
> par(new=T)
> rect(-4,-4,0,0,col='#ddddff')
> par(new=T)
> rect(0,-4,4,0,col='#ffdddd')
> par(new=T)
> plot(xorc[,-3],col=c(rep('blue',50),rep('red',50)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2.5)
> par(new=T)
> contour(px,py,array(predict(xorc.gdbt,newdata=dpgrid1),dim = c(length(px),length(py))),levels = 0.5,drawlabels = T,col='purple',lwd=6,xlim=c(-4,4),ylim=c(-4,4))

f:id:TJO:20150604155924p:plain:w250 f:id:TJO:20150604155934p:plain:w250

Results look very nice:) On simple XOR pattern, Xgboost provides simple decision boundaries as the same as Decision Tree. On the other hand, it provides really complicated decision boundaries on complex XOR pattern, but its boundaries are somewhat following the assumed true boundaries. It implies Xgboost can get well generalized, in particular in comparison with Random Forest.

Let's see how parameter tuning affects decision boundaries.

> # More overfitted
> xorc.gdbt<-xgb.train(params=list(objective="binary:logistic",eval_metric="logloss",eta=1,max_depth=8),data=dxorc,nrounds=100)
> plot(c(),type='n',xlim=c(-4,4),ylim=c(-4,4))
> par(new=T)
> rect(0,0,4,4,col='#ddddff')
> par(new=T)
> rect(-4,0,0,4,col='#ffdddd')
> par(new=T)
> rect(-4,-4,0,0,col='#ddddff')
> par(new=T)
> rect(0,-4,4,0,col='#ffdddd')
> par(new=T)
> plot(xorc[,-3],col=c(rep('blue',50),rep('red',50)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2.5)
> par(new=T)
> contour(px,py,array(predict(xorc.gdbt,newdata=dpgrid1),dim = c(length(px),length(py))),levels = 0.5,drawlabels = T,col='purple',lwd=5,xlim=c(-4,4),ylim=c(-4,4))

> # More generalized
> xorc.gdbt<-xgb.train(params=list(objective="binary:logistic",eval_metric="logloss",eta=0.1,max_depth=4),data=dxorc,nrounds=100)
> plot(c(),type='n',xlim=c(-4,4),ylim=c(-4,4))
> par(new=T)
> rect(0,0,4,4,col='#ddddff')
> par(new=T)
> rect(-4,0,0,4,col='#ffdddd')
> par(new=T)
> rect(-4,-4,0,0,col='#ddddff')
> par(new=T)
> rect(0,-4,4,0,col='#ffdddd')
> par(new=T)
> plot(xorc[,-3],col=c(rep('blue',50),rep('red',50)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2.5)
> par(new=T)
> contour(px,py,array(predict(xorc.gdbt,newdata=dpgrid1),dim = c(length(px),length(py))),levels = 0.5,drawlabels = T,col='purple',lwd=5,xlim=c(-4,4),ylim=c(-4,4))

f:id:TJO:20150604155952p:plain:w250 f:id:TJO:20150604160004p:plain:w250

Despite a slight difference, it found that parameter tuning can well control a degree of overfitting / generalization. Indeed too much generalization on Xgboost model results in too much simple decision boundaries (almost the same as boundaries by Decision Tree on simple XOR pattern).

Next, let's see how Xgboost works on linearly separable patterns.

# Set up datasets of linearly separable patterns
> dbi<-read.table("linear_bi.txt",header=T)
> dml<-read.table("linear_multi.txt",header=T)

# Set up another grid
> px2<-seq(-0.5,4.5,0.03)
> py2<-seq(-0.5,4.5,0.03)
> pgrid2<-expand.grid(px2,py2)
> names(pgrid2)<-names(dbi)[-3]

# Convert them into sparse.model.matrix
> dbi.mx<-sparse.model.matrix(label~.,dbi)
> dml.mx<-sparse.model.matrix(label~.,dml)
> pgrid2.mx<-sparse.model.matrix(~.,pgrid2)

# Convert them further into xgb.DMatrix
> ddbi<-xgb.DMatrix(dbi.mx,label=dbi$label)
> ddml<-xgb.DMatrix(dml.mx,label=dml$label)
> dpgrid2<-xgb.DMatrix(pgrid2.mx)

# Train models with xgb.train() function
> dbi.gdbt<-xgb.train(params=list(objective="binary:logistic",eval_metric="logloss"),data=ddbi,nrounds=100)
> dml.gdbt<-xgb.train(params=list(objective="multi:softmax",num_class=3,eval_metric="mlogloss"),data=ddml,nrounds=100)
# In case of multi-class training, "objective" should be "multi:softmax" or "multi:softprob" and "num_class"should be given

# 2-classes linearly separable patterns
> plot(c(),type='n',xlim=c(-0.5,3.5),ylim=c(-0.5,3.5))
> par(new=T)
> polygon(c(-0.5,-0.5,3.5),c(3.5,-0.5,-0.5),col='#ddddff')
> par(new=T)
> polygon(c(-0.5,3.5,3.5),c(3.5,-0.5,3.5),col='#ffdddd')
> par(new=T)
> plot(dbi[,-3],pch=19,col=c(rep('blue',25),rep('red',25)),cex=3,xlim=c(-0.5,3.5),ylim=c(-0.5,3.5))
> par(new=T)
> contour(px2,py2,array(predict(dbi.gdbt,newdata=dpgrid2),dim = c(length(px2),length(py2))),xlim=c(-0.5,3.5),ylim=c(-0.5,3.5),lwd=6,col='purple',levels = 0.5,drawlabels = T)

# 3-classes linearly separable patterns
> plot(c(),type='n',xlim=c(-0.5,4.5),ylim=c(-0.5,4.5))
> par(new=T)
> polygon(c(-0.5,-0.5,3.5),c(3.5,-0.5,-0.5),col='#ddddff')
> par(new=T)
> polygon(c(-0.5,3.5,4.5,4.5,1.0,-0.5),c(3.5,-0.5,-0.5,1.0,4.5,4.5),col='#ffdddd')
> par(new=T)
> polygon(c(1.0,4.5,4.5),c(4.5,1.0,4.5),col='#ddffdd')
> par(new=T)
> plot(dml[,-3],pch=19,col=c(rep('blue',25),rep('red',25),rep('green',25)),cex=3,xlim=c(-0.5,4.5),ylim=c(-0.5,4.5))
> par(new=T)
> contour(px2,py2,array(predict(dml.gdbt,newdata=dpgrid2),dim=c(length(px2),length(py2))),xlim=c(-0.5,4.5),ylim=c(-0.5,4.5),col="purple",lwd=6,drawlabels=T,levels=c(0.5,1.5))

f:id:TJO:20150604160027p:plain:w250 f:id:TJO:20150604160037p:plain:w250

OMG, stop joking... both decision boundaries by Xgboost seem to never follow the assumed true boundaries, similarly to Random Forest and Decision Tree. Like those tree models, Xgboost also has difficulty in classifying linearly separable patterns.

Conclusions

In this post, we learned important lessons below:

Learning of Xgboost is greedier than the other boosting methods and (perhaps) other classifiers
In general, classification models with Xgboost are well generalized (more than Random Forest), but depending on parameter tuning
Like other tree models, Xgboost is not good at classifying linearly separable patterns

Personally I think the fact that generalization of Xgboost is stronger than Random Forest is the most important in practical use. In many industrial missions, indeed Random Forest has been preferred because of its simple implementation, speed and other convenient features such as computing variable importance. But I guess more and more people may start to use Xgboost instead of Random Forest, and actually many competitors in Kaggle use it.

In that sense, Xgboost can be the next de-facto standard classifier in coming couples of years I think. How do you think? :P)

*1:max_depth in {xgboost}

*2:eta in {xgboost}

*3:subsample in {xgboost}