Machine learning for package users with R (1): Decision Tree

Notice

Currently {mvpart} CRAN package was removed from CRAN due to expiration of its support. For installation, 1) please download the latest (but expired) package archive from the old archive site and 2) install it following the procedure shown below.

In short, for Mac or Linux R command below will work.

> install.packages("[URL of the pacakges' tar.gz here]", repos=NULL, type="source")

For Windows, first you have to edit PATH to include R folder, and then please type as below on Command Prompt or PowerSchell.

R CMD INSTALL XYZ.tar.gz

In the previous post, we saw how to evaluate a machine learning classifier using typical XOR patterns and drawing its decision boundary on the same XY plane. In this post, let's see how Decision Tree, one of the lightest machine learning classifier, works.

A brief trial on a short version of MNIST datasets

I think it's good to see how each classifier works on the typical MNIST datasets. Prior to writing this post, I prepared a short version of MNIST datasets and uploaded onto my GitHub repository below.

Please download 'short_prac_train.csv' and 'short_prac_test.csv' onto your R working folder and run as below.

> train<-read.csv("short_prac_train.csv", header=TRUE)
> test<-read.csv("short_prac_test.csv", header=TRUE)
> library(mvpart)
# If you didn't install it, please refer the top of this post and install {mvpart} package
> train$label<-as.factor(train$label)
> test$label<-as.factor(test$label)
> train.rp<-rpart(label~.,train)
> plotcp(train.rp)
# CP plot indicated (maybe) no pruning is required
> table(test$label,predict(train.rp,newdata=test[,-1],type='vector'))
   
     1  2  3  4  5  6  7  8  9 10
  0 86  0  0  2  0  1  0  9  1  1
  1  0 82  1  3  0  0  1  4  9  0
  2  4  9 49  4  0  0  8 12 13  1
  3  5  4  0 57  0  1  0  4 14 15
  4  0  1  0  5 48  3  5 12  1 25
  5  5  3  1 20  9 26  8  6  5 17
  6  2  3  1  6  1  2 61 15  4  5
  7  3  1  1  1  0  0  0 78  5 11
  8  0  8  0  3  3  0  2  9 64 11
  9  0  2  0  8  1  6  1 19  3 60

> sum(diag(table(test$label,predict(train.rp,newdata=test[,-1],type='vector'))))/nrow(test)
[1] 0.611
# Oops, very low accuracy...

OMG, but don't worry; Decision Tree works better with various ensemble methods rather than itself alone.

Algorithm summary

In general, the word "Decision Tree" may be referred to CART, a representative algorithm of Decision Tree. It can be summarized as below*1:

1. While searching independent variables of the samples based on a certain criterion (e.g. Gini index),
2. the algorithm determines how to split them in order both to make a "purity" of the samples with dependent and independent variables at each step and to exclude "deviant" sample sets from the rest and,
3. repeats the same procedure,
4. it finished if a certain terminal condition is satisfied,
5. until all splitting procedure are terminated.

At any rate, such an algorithm with multiple splitting results in a "tree" shaped classification structure, that's why this algorithm is called Decision "Tree".

Of course almost the same procedure can be applied to regression problems and in such a case it's called "Regression Tree". Unlike the other regression methods, regression tree produces step-like regression functions.

How it works on XOR patterns

Next, let's see what kind of decision boundary Decision Tree draws. Please download "xor_simple.txt" and "xor_complex.txt" from the repository below.

Second, please preprocess them as below.

> xors<-read.table("xor_simple.txt", header=T)
> xorc<-read.table("xor_complex.txt",header=T)
> xors$label<-as.factor(xors$label-1)
> xorc$label<-as.factor(xorc$label-1)

Now all ready. Let's run as below!

Drawing decision boundaries

# Trained a decision tree by rpart() function of {mvpart} package
> xors.rp<-rpart(label~.,xors)

# Prepared a grid
> px<-seq(-4,4,0.3)
> py<-seq(-4,4,0.3)
> pgrid<-expand.grid(px,py)
> names(pgrid)<-names(xors)[-3]

# Plot it - decision tree for the simple XOR pattern
> plot(c(),type='n',xlim=c(-4,4),ylim=c(-4,4))
> par(new=T)
> rect(0,0,4,4,col='#aaaaff')
> par(new=T)
> rect(-4,0,0,4,col='#ffaaaa')
> par(new=T)
> rect(-4,-4,0,0,col='#aaaaff')
> par(new=T)
> rect(0,-4,4,0,col='#ffaaaa')
> par(new=T)
> plot(xors[,-3],col=c(rep('blue',50),rep('red',50)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2.5)
> par(new=T)
> contour(px,py,array(predict(xors.rp,newdata=pgrid),dim=c(length(px),length(py))),xlim=c(-4,4),ylim=c(-4,4),col="purple",lwd=5,drawlabels=T,levels=0.5)

Yeah, it's perfect! On the other hand, how about for the complex XOR pattern?

# Train a decision tree for the complex XOR pattern
> xorc.rp<-rpart(label~.,xorc)
> plot(c(),type='n',xlim=c(-4,4),ylim=c(-4,4))
> par(new=T)
> rect(0,0,4,4,col='#aaaaff')
> par(new=T)
> rect(-4,0,0,4,col='#ffaaaa')
> par(new=T)
> rect(-4,-4,0,0,col='#aaaaff')
> par(new=T)
> rect(0,-4,4,0,col='#ffaaaa')
> par(new=T)
> plot(xorc[,-3],col=c(rep('blue',50),rep('red',50)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2.5)
> par(new=T)
> contour(px,py,array(predict(xorc.rp,newdata=pgrid),dim=c(length(px),length(py))),xlim=c(-4,4),ylim=c(-4,4),col="purple",lwd=5,drawlabels=T,levels=0.5)

Oh my god, what's going on??? This decision boundary looks much crazy... it almost never follows the assumed true boundary.

Pruning

Please remember I defined this kind of decision boundary as "overfitted". If so, we have to make it "generalized"... how can we do so for the classifier?

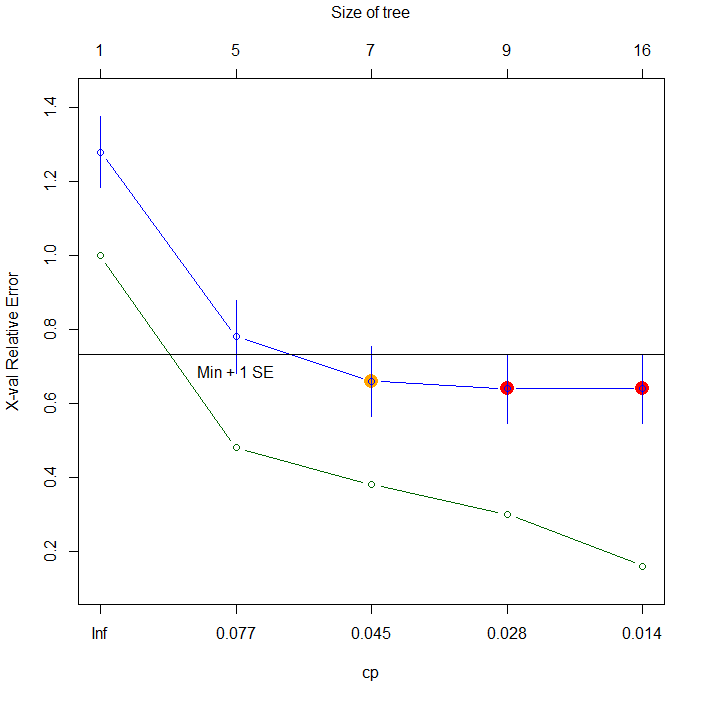
The primary solution for decision tree is "pruning": a method with evaluating complexity of the tree based on its cross-validation error rate and determining a hyper parameter for the best model. In {mvpart} package, we can run it with plotcp() function and "cp" argument of rpart() function.

# Run a cross-validation procedure for pruning
> plotcp(xorc.rp) # cp=0.045 looks the best

# Prune the tree
> xorc.rp2<-rpart(label~.,xorc,cp=0.045)

# Plot it
> plot(c(),type='n',xlim=c(-4,4),ylim=c(-4,4))
> par(new=T)
> rect(0,0,4,4,col='#aaaaff')
> par(new=T)
> rect(-4,0,0,4,col='#ffaaaa')
> par(new=T)
> rect(-4,-4,0,0,col='#aaaaff')
> par(new=T)
> rect(0,-4,4,0,col='#ffaaaa')
> par(new=T)
> plot(xorc[,-3],col=c(rep('blue',50),rep('red',50)),xlim=c(-4,4),ylim=c(-4,4),pch=19,cex=2.5)
> par(new=T)
> contour(px,py,array(predict(xorc.rp2,newdata=pgrid),dim=c(length(px),length(py))),xlim=c(-4,4),ylim=c(-4,4),col="purple",lwd=5,drawlabels=T,levels=0.5)

I feel it's still a little overfitted, but at any rate it got a little more generalized, i.e. some meaningless decision boundaries were removed from the previous model.

How it works on linearly separable patterns

As you see as above, decision tree can classify linearly non-separable patterns. But you may wonder how it works on usual linearly separable patterns. OK, let's see it. Please download "linear_bi.txt" and "linear_multi.txt" from the GitHub repository mentioned above and import them.

> dbi<-read.table("linear_bi.txt",header=T)
> dml<-read.table("linear_multi.txt",header=T)
> dbi$label<-as.factor(dbi$label)
> dml$label<-as.factor(dml$label)

OK, let's run them.

# Train decision trees for 2-classes and 3-classes patterns
> dbi.rp<-rpart(label~.,dbi)
> dml.rp<-rpart(label~.,dml)

# Prepare a grid
> px2<-seq(-0.5,4.5,0.1)
> py2<-seq(-0.5,4.5,0.1)
> pgrid2<-expand.grid(px2,py2)
> names(pgrid2)<-names(pgrid)

# Plot them
# 2-classes
> plot(c(),type='n',xlim=c(-0.5,3.5),ylim=c(-0.5,3.5))
> par(new=T)
> polygon(c(-0.5,-0.5,3.5),c(3.5,-0.5,-0.5),col='#aaaaff')
> par(new=T)
> polygon(c(-0.5,3.5,3.5),c(3.5,-0.5,3.5),col='#ffaaaa')
> par(new=T)
> plot(dbi[,-3],pch=19,col=c(rep('blue',25),rep('red',25)),cex=3,xlim=c(-0.5,3.5),ylim=c(-0.5,3.5))
> par(new=T)
> contour(px2,py2,array(predict(dbi.rp,newdata=pgrid2),dim=c(length(px2),length(py2))),xlim=c(-0.5,3.5),ylim=c(-0.5,3.5),col="purple",lwd=3,drawlabels=T,levels=0.5)

# 3-classes
> plot(c(),type='n',xlim=c(-0.5,4.5),ylim=c(-0.5,4.5))
> par(new=T)
> polygon(c(-0.5,-0.5,3.5),c(3.5,-0.5,-0.5),col='#aaaaff')
> par(new=T)
> polygon(c(-0.5,3.5,4.5,4.5,1.0,-0.5),c(3.5,-0.5,-0.5,1.0,4.5,4.5),col='#ffaaaa')
> par(new=T)
> polygon(c(1.0,4.5,4.5),c(4.5,1.0,4.5),col='#ccffcc')
> par(new=T)
> plot(dml[,-3],pch=19,col=c(rep('blue',25),rep('red',25),rep('green',25)),cex=3,xlim=c(-0.5,4.5),ylim=c(-0.5,4.5))
> par(new=T)
> contour(px2,py2,array(predict(dml.rp,newdata=pgrid2,'vector'),dim=c(length(px2),length(py2))),xlim=c(-0.5,4.5),ylim=c(-0.5,4.5),col="purple",lwd=5,drawlabels=T,levels=c(1.5,2.5))

Although decision tree well works for both XOR patterns, it shows strong overfitting or bad performance for both linearly separable patterns.

Conclusions

We have two important lessons here as below:

1. Decision tree requires pruning via cross-validation tests
2. It works well on linearly non-separable patterns, although really bad for linearly separable patterns

Of course these results don't always work for all of classification problems as Bishop pointed out in his representative seminar book, but it should be considered more than ever for everybody.

*1:I know my English here gets a little confused...