Can multivariate modeling predict taste of wine? Beyond human intuition and univariate reductionism
At a certain meetup on the other day, I talked about a brand-new relationship between taste of wine (i.e. professional tasting) and data science. This talk was inspired by a book "Wine Science: The Application of Science in Winemaking". Below is its Japanese edition.

- 作者: ジェイミーグッド,Jamie Goode,梶山あゆみ
- 出版社/メーカー: 河出書房新社
- 発売日: 2014/11/12
- メディア: 単行本
- この商品を含むブログを見る
For readers who can't read Japanese, I summarized the content of the talk in this post. Just for your information, I myself am a super wine lover :) and I'm also much interested in how data science explain taste of wine.
In order to run analytics below, I prepared an R workspace in my GitHub repository. Please download and import it into your R environment.
(Note: All quotes from Goode's book here are reversely translated from the Japanese edition and it may contain not a few difference from the original version)
Efforts to make wine tasting "scientific", described in Goode's book
Goode's book has three chapters: science of viticulture, science of brewing, and science of taste of wine. I'm much interested in also the content of the former two chapters, but main interest here is the third chapter. "How can we make wine tasting so scientific?"
Indeed science of wine tasting has a long-lasting history. As written in Goode's book, first people have categorized taste of wine into several components, such as sweet, acid, tannic, etc., and second people have looked for any ingredients that enable us to predict whether the wine is tasty or not, for many years.
According to Goode's book, in general wine contains twenty kinds of chemical compounds related to its fundamental flavor and taste. But further interestingly, only a compound is included in a grape berry: nineteen are elaborated by yeast through its fermentation processes. In addition, sixteen compounds are known to indirectly contribute to the flavor and taste, and some very rare compounds are known as "impact compounds" that influence the flavor and taste drastically despite its further little amount.
In short, taste and flavor of wine should be given by an ensemble of these chemical compounds. This fact leads to an idea that we can score each wine by checking such chemical compounds without actual tasting. It would be very important because even Wine Advocate or Wine Spectator cannot all of wines in the world: I believe some of newly released wines, less known wines or very rare wines may be neglected by them. Such wines cannot be evaluated and will have no score by them. Consequently consumers cannot imagine whether those are good and don't dare to buy them. That is a tragedy.
However, some problems remain. Goode's book warns as below.
These kinds of researches enhance an importance of a holistic view on each wine. If one wants to study taste and flavor of wine in a reductionistic manner, one must decompose the wine into several components and investigate each component individually. However, researchers have come to think such an approach has a serious limitation.
"Everybody were trying to simplify everything at any rate. They argued that first distinguishing each component from its whole content, second focusing on each one, and then this compound is important for something, because when there is the one it exceeds a threshold, and so on. But actually it doesn't make sense when we pick up one compound and argue about each threshold because any manipulation affects several other components at once"
Quality means a characteristic of a whole system. An ensemble of individual components of wine enables us to experience a feeling of tasting wine. It cannot be understood by studying each component separately.
If we want to develop science of wine and to understand a quality of wine further deeper, we should remove a restriction on our analytical approach merely based on reductionalism. We should also understand an experience of tasting wine with a holistic view.
(Reversely translated from pp.387-401 of the Japanese edition)
I agree these arguments. For example, let's see alcohol content; just in general, people love high alcohol wines. But from my own experience, high alcohol but less acid wines can be somewhat rude. On the other hand, even though high alcohol and more acid, wines with less residual sugar can be not good because of its excessive acidity. So, how about a wine with high alcohol, more acid and rich residual sugar? Hmm, it can be a failed noble rot wine...
In short, what I emphasize here is that focusing on a single component has a serious limitation. I understand why Goode described it as a kind of "limitation of reductionism".
Reductionism = univariate analysis?
I think readers now understand what's going on about this issue. OK, let's drill down with a practical analytics using R. The dataset "Wine Quality" originally provided by UCI machine learning repository contains variables as below.
- fixed acidity
- volatile acidity
- citric acid
- residual sugar
- chlorides
- free sulfur dioxide
- total sulfur dioxide
- density
- pH
- sulphates
- alcohol
- quality (dependent variable: range 3-8)
We can easily see a relationship between a specific independent variable and quality (tasting score) using a simple correlation analysis. For example, let's plot a scattergram with alcohol and quality, and draw a simple regression line by hand.

It implies that more alcohol, more quality. More alcohol, further tasty wine? Yes, it sounds pretty nice and very intuitive. In order to check whether the simple model "more alcohol, more tasty wine", let's run an univariate regression.
> alc.lm<-lm(quality~alcohol,d.train) > table(d.test$quality,round(predict(alc.lm,newdata=d.test[,-12]),0)) 5 6 7 3 0 1 0 4 4 0 1 5 52 16 0 6 21 43 0 7 1 18 1 8 0 1 1 > (52+43+1)/160 [1] 0.6
Accuracy 60% sounds - hmm... - not so good. Indeed, a confusion matrix above also shows some wines record lower tasting score despite high alcohol content. This simple model cannot rule them out. OK, how about plotting all of scattergrams between quality and other independent variables?

OMG, it looks too much confusing :((( This kind of analysis is useless, because it's beyond our intuition. This is what Goode pointed out in his book; a limitation of reductionism, and a holistic approach required. If so, how can we do that?
Multivariate modeling can predict which wine is good
I think readers of this blog may have a good answer to it; multivariate modeling, such as statistical modeling (linear models / GLM / Bayesian modeling) or machine learning. These methods handle not only a single variable but also multiple variables at once in order to build a model that can explain a behavior of a dependent variable, with counterbalancing independent variables.
For example, random forest would be a good example to understand how effectively such a kind of multivariate modeling works on multivariate datasets. Let's run it on R as below.
> library(randomForest) # Tune a random forest classifier > tuneRF(d.train[,-12],as.factor(d.train[,12]),doBest=T) mtry = 3 OOB error = 30.65% Searching left ... mtry = 2 OOB error = 31.2% -0.01814059 0.05 Searching right ... mtry = 6 OOB error = 31.62% -0.03174603 0.05 Call: randomForest(x = x, y = y, mtry = res[which.min(res[, 2]), 1]) Type of random forest: classification Number of trees: 500 No. of variables tried at each split: 3 OOB estimate of error rate: 29.26% Confusion matrix: 3 4 5 6 7 8 class.error 3 0 1 7 1 0 0 1.0000000 4 1 0 28 18 1 0 1.0000000 5 0 1 499 110 3 0 0.1859706 6 0 0 121 426 27 0 0.2578397 7 0 0 7 81 91 0 0.4916201 8 0 0 0 8 6 2 0.8750000 # mtry=3 is the best # quality (dependent variable) is cast to factor and train a random forest classifier > d.train.factor.rf<-randomForest(as.factor(quality)~.,d.train,mtry=3) # confusion matrix > table(d.test$quality,predict(d.train.factor.rf,newdata=d.test[,-12])) 3 4 5 6 7 8 3 0 0 1 0 0 0 4 0 0 4 1 0 0 5 0 0 58 10 0 0 6 0 1 12 48 3 0 7 0 0 1 4 15 0 8 0 0 0 0 2 0 > (58+48+15)/160 [1] 0.75625 # accuracy
More than 75% accuracy is a somewhat large improvement from the original one given by the univariate model of alcohol content. This fact means that multivariate modeling like random forest can predict tasting score of wine better than a simple univariate and intuitive criterion. As well known, random forest can compute an importance of variables that shows which variable is more influential. Let's see it.
> importance(d.train.factor.rf) MeanDecreaseGini fixed.acidity 69.60611 volatile.acidity 97.57508 citric.acid 68.37856 residual.sugar 65.64702 chlorides 75.12833 free.sulfur.dioxide 61.07482 total.sulfur.dioxide 94.10219 density 87.32159 pH 69.21815 sulphates 102.46872 alcohol 133.72922
The result shows that alcohol, sulphates, volatile acidity and total sulfur dioxide are more influential on quality (tasting score) than other variables. However, this result alone cannot identify which variable positively correlates to quality or which variable negatively. To identify those, let's estimate a simple multiple linear regression model although it's accuracy would be lower.
> summary(lm(quality~.,d.train)) Call: lm(formula = quality ~ ., data = d.train) Residuals: Min 1Q Median 3Q Max -2.7256 -0.3538 -0.0470 0.4541 1.9565 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 12.6307205 22.2671936 0.567 0.570644 fixed.acidity 0.0130328 0.0270194 0.482 0.629633 volatile.acidity -1.1794967 0.1274792 -9.252 < 2e-16 *** citric.acid -0.1838340 0.1544325 -1.190 0.234093 residual.sugar 0.0073885 0.0156617 0.472 0.637173 chlorides -1.6444079 0.4414953 -3.725 0.000203 *** free.sulfur.dioxide 0.0048293 0.0022897 2.109 0.035103 * total.sulfur.dioxide -0.0030132 0.0007693 -3.917 9.40e-05 *** density -8.3935917 22.7154552 -0.370 0.711802 pH -0.4270140 0.2005306 -2.129 0.033390 * sulphates 0.9683204 0.1226886 7.893 5.86e-15 *** alcohol 0.2781216 0.0277798 10.012 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.6456 on 1427 degrees of freedom Multiple R-squared: 0.3655, Adjusted R-squared: 0.3606 F-statistic: 74.73 on 11 and 1427 DF, p-value: < 2.2e-16
Now we can see 1) higher alcohol or sulphates raises quality and 2) lower volatile acidity or total sulfur dioxide raises quality. But whether their effects are linear or not is unclear. As mentioned above, a balance between acidity and sweetness would be much important for its taste and they may have some threshold. To quantify it, let's train a random forest regressor and visualize with partial dependence plot using partialPlot function. Instead of total sulfur dioxide, pH is added to the variables.
# Tune a random forest with a numeric dependent variable > tuneRF(d.train[,-12],d.train[,12],doBest=T) mtry = 3 OOB error = 0.3407737 Searching left ... mtry = 2 OOB error = 0.3548686 -0.04136142 0.05 Searching right ... mtry = 6 OOB error = 0.3396589 0.003271477 0.05 Call: randomForest(x = x, y = y, mtry = res[which.min(res[, 2]), 1]) Type of random forest: regression Number of trees: 500 No. of variables tried at each split: 6 Mean of squared residuals: 0.3225541 % Var explained: 50.49 # mtry=6 is the best # Train a random forest regressor > d.train.numeric.rf<-randomForest(quality~.,d.train,mtry=6) > table(d.test$quality,round(predict(d.train.numeric.rf,newdata=d.test[,-12]),0)) 5 6 7 3 1 0 0 4 3 2 0 5 56 12 0 6 16 45 3 7 1 9 10 8 0 0 2 > (56+45+10)/160 [1] 0.69375 # Accuracy decreases a little > par(mfrow=c(2,2)) > partialPlot(d.train.numeric.rf,d.train,x.var=alcohol) > partialPlot(d.train.numeric.rf,d.train,x.var=sulphates) > partialPlot(d.train.numeric.rf,d.train,x.var=volatile.acidity) > partialPlot(d.train.numeric.rf,d.train,x.var=pH)
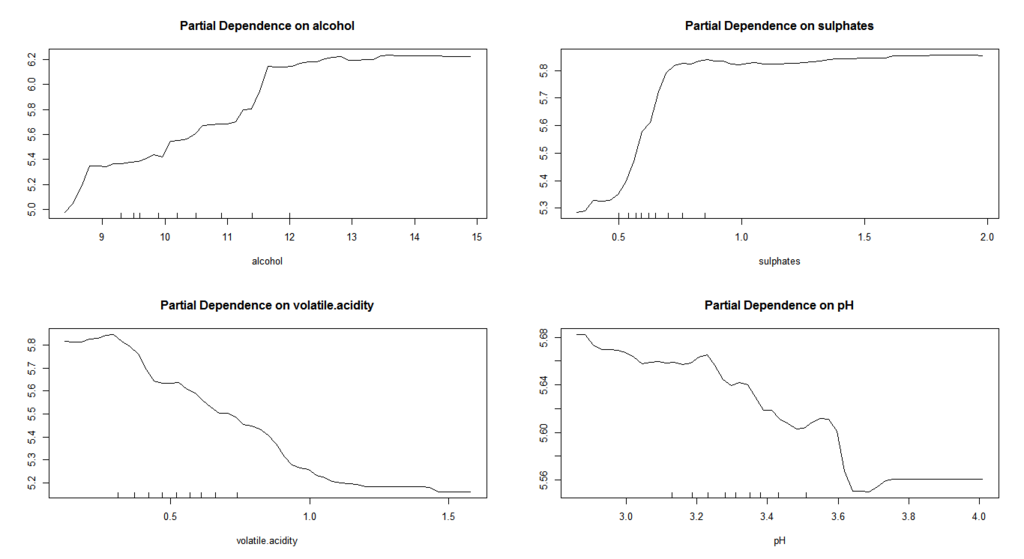
These results are very interesting. Effects on tasting score from alcohol and sulphates are positively linear but get saturated at certain threshold. On the other hand, an effect from volatile acidity is negatively linear without solid threshold. A behavior of pH is very interesting: it shows some local peaks and entirely nonlinear. Although its accuracy of prediction is a little lower than that of a random forest classifier, these partial dependence plots imply some complicated and nonlinear dynamics across ingredients behind taste of wine.
Conclusions
The lessons we learn in this post are:
- Univariate modeling (including a simple criterion with simple threshold or univariate regression) is intuitive and easy to understand, but it cannot precisely predict tasting score of wine
- Multivarate modeling such as statistical models or machine learning successfully predict tasting score of wine from multivariate datasets with chemical compounds in wine
- Deeper analysis using random forest implies some complicated and nonlinear dynamics across such ingredients behind taste of wine
I think that a phrase "limitation of reductionism" described in Goode's book means merely a limitation of univariate modeling and multivariate modeling can go beyond it. I'm not any expert in wine industry so I don't know much about the current situation of any studies on relationship between chemical ingredients and taste of wine so far, but I hope modern multivariate modeling techniques such as machine learning will facilitate "holistic view" on taste of wine.